机器人奇异性介绍

修订日期	修订版本	修订内容	修订人
2024.3.14	v0.1	初始化文档	袁紫衣
2024.3.20	v0.2	增加控制部分	高振宇
2024.3.21	v0.3	增加规划部分	赵锦强

[TOC]

1. 什么是奇异点

通常说的奇异即运动学奇异（kinematic singularity）： 是指在其在构型空间中，存在某一构型，使得其对应雅克比矩阵的秩维度减少，机器人末端在一个或多个方向，失去了运动的能力。

运动学奇异点的出现通常与机器人的运动学参数和几何结构有关，从机构学（线几何）来讲，常见的运动学奇异包括以下几种：

两个或多轴共线
三轴或多轴共面且平行
四个旋转关节轴线交于一点
四个旋转轴共面
六个旋转关节轴相交于一条公共线

AUBO-I 系列的运动学奇异点

机器人的运动学奇异可以通过雅克比矩阵是否满秩（行列式是否为0）来进行判断:

对于 AUBO-I 系列，其雅克比的行列式的值的表达式为：

detJ = (a2 * sin(q2) + a3 * sin(q2 - q3) + d5 * sin(q2 - q3 + q4))*sin(q3)*sin(q5); // 其中a2,a3,d5为结构参数

存在三种奇异构型：

$q_3 = 0$ ，称为 肘部奇异(Wrist Singularity)

会导致关节2,3,4三个轴线共面且平行，从而导致第二种奇异
$q_5 = 0$ , 称为 腕部奇异(Elbow Singularity)

会导致2,3,4,6关节轴平行，交于无穷远处；从而导致第三种奇异；
5,6 轴的交点在1,2关节轴组成的平面时：称为内部奇异

AUBO-I 系列的工作空间

AUBO-I 系列机器人的工作空间是球形的，在球形的边界为工作空间的最大范围。在工作空间的中心，底座关节的正上方和正下方有一个圆柱，该圆柱内部区域也是不可到达的区域，圆柱半径为 $d_2-d_6$ ，以下是 AUBO-I5 机器人工作空间示意图：

当机器人末端到达外部边界时，肘部和腕部均处于奇异状态
当机器人末端到达内部边界时，处于内部奇异状态

2 奇异点会产生什么问题

机器人在奇异点附近（奇异空间）运动会导致在运动控制或力控制中，失去某个或多个方向的自由度，运动不稳定，精度降低，控制困难等问题。

逆运动学与奇异空间

AUBO-I 系列机器人逆运动学求解失败主要包括以下两个原因：

机器人在物理上无法到达所需位置，目标点位不在工作空间内
机器人处于奇异构型

工作空间内的逆运动学

已知机器人末端位姿反求关节角
- 非线性方程（三角函数）导致的无解、多解、无穷多解
  - 对于AUBO I系列构型非奇异空间内最多存在8个解
- 奇异点通常是无解和无穷多解的情况
  - 从解析解角度讲：(如因除0)不能求出每个关节角，但可以求出一些关节角的线性组合，理论上存在无穷多组解或无解
  - 从迭代解的角度讲：奇异空间是包含奇异点附近的空间，此时雅克比矩阵病态，迭代逆解计算误差精度降低
已知末端速度反求关节速度
- 速度映射关系： $V_e = J(\theta)*\dot \theta$ $V^{ e } = J (θ) * θ ˙ $ 矢量 $\theta,V_e,\dot\theta$ $θ, V^{ e }, θ ˙ $ 分别为关节角、末端速度（含角速度）、关节速度。
  - 奇异空间内雅克比阵 $J$ 病态甚至不可逆，此时不能准确的计算出关节速度。
  - 属于雅克比矩阵零空间的 $\dot \theta$ 无论多大都不会对末端速度产生影响。换句话说，在奇异空间附近末端速度即使很小也可能导致关节速度过大。
  - 从过速的角度看，通常奇异点出现在机械臂失去自由度的情况，如关节3角度为0或180度。
  - 对AUBO机器人来说，雅克比矩阵的秩最小为3，此时对应的奇异空间最难处理。

力与奇异空间

力域中的雅克比： $T = J^T(q)*F$ , $F$ 为施加在关节末端的力和扭矩矢量， $T$ 为各关节所需平衡力矩。 $J^T$ 为前面介绍的雅克比阵转置。

力域中与运动学中的奇异点一致，因为 $J$ 和 $J^T$ 的行列式相同。
$F$ $F$ 对机械臂的影响：
- 如果 $F$ 属于 $J^T$ 的零空间，无论多大的 $F$ 都不会在各个关节产生扭矩，会被机械结构限制所消耗。
- 如果 $F$ 正交于 $J^T$ 的零空间，则末端会沿着 $F$ 的方向无误差的运动。
- 如果 $F$ 介于上述两种情况之间，则末端会 $F$ 沿 $J^T$ 的非零空间投影方向移动。

3 如何规避奇异点

3.1 逆运动学与奇异规避

在机器人执行任务时，应避免在工作空间边界工作，如果无法避免，在附近区域尽量使用 MoveJ，而不是 MoveL。
解析逆解：理论上存在无穷多组解或无解
迭代逆解：迭代逆精度会降低

可以采用以下方法处理雅克比矩阵病态的问题：
- 阻尼最小二乘算法
- 雅克比转置矩阵算法
- 基于 SVD 分解算法

参考论文：

Overview of Damped Least-Squares Methods for Inverse Kinematics of Robot Manipulators

Singularity-Consistent Parameterization of Robot Motion and Control

SINGULARITY CONSISTENT INVERSE KINEMATICS BY ENHANCING THE JACOBIAN TRANSPOSE

3.2 轨迹规划与奇异规避

轨迹规划中奇异规避采用以下两种方法（主要参考doosan robot的设计方法）：

奇异防护转化为最大速度约束

根据关节最大运动速度和关节极限位置限制，实时计算机械臂运动过程中关节的运动能力

根据关节空间最大和最小速度，以及笛卡尔空间运动方向，实时计算在指定构型下的笛卡尔最大速度

/**
     * @brief 计算在指定构型下的笛卡尔空间最大线速率和最大角速率(如果当前的速率为零, 则返回的是绕X轴方向的最大速率)
     * @param jac: 传入的雅克比矩阵(在指定构型下的TCP相对Base的几何雅克比)
     * @param max_joint_velocity: 关节最大速度
     * @param min_joint_velocity: 关节最小速度
     * @param cur_cartesian_velocity: 当前速度(TCP在Base下的描述)
     * @return: 返回笛卡尔空间的最大速率(第一个维度表示移动, 第二个维度表示转动)
     */
Vector2d calMaxCartesianVelocity(const Jacobian& jac, const JntArray& max_joint_velocity, const JntArray& min_joint_velocity, const Twist& cur_cartesian_velocity) = 0;

对机械臂进行动态调速，避免在奇异位置关节超速

躲避规划：运动过程中若靠近奇异位置附近，机械臂自主进行躲避规划，在远离奇异位置后回到原路径进行运动

3.3 力控与奇异规避

力控中奇异规避采用以下3种方法:

奇异防护转化为变导纳参数设计

控制器输入之前，建立奇异指标与导纳参数之间的映射关系
- 使用一种新的指数衰减最小二乘法（EDLS）来处理 Singularity。这种方法可以平滑地减小机器人在 Singularity 方向上的运动，从而避免不稳定的运动
- 使用一种非对称阻尼方案，当机器人远离 Singularity 时减小阻尼，从而改善了机器人的响应能力，提高了操作员的交互体验
具体的阻尼方法也可以使用模糊规则进行设计
奇异防护转化为虚拟力设计

控制器输入之前，建立奇异指标与虚拟力之间的映射关系，虚拟力的设计要考虑远离还是接近奇异点
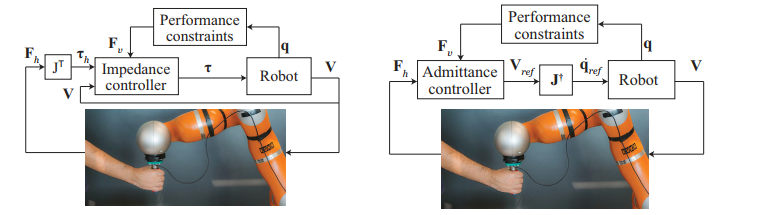
奇异防护转化为最大速度约束

控制器输出之后，将奇异问题转化为笛卡尔空间Base坐标下的最大速度约束问题，一般来说
- 关节空间最大速度 $\dot{q}_{max}$ 有两个来源:
  - 用户输入
  - 电机最大运动能力
- 笛卡尔空间最大速度 $\dot{X}_{max}$ 有两个来源:
  - 用户输入
  - 关节空间映射
其中，关节空间映射到笛卡尔空间最大速度由正运动学 $\dot{X}_{max}=J \dot q_{max}$ 计算，当机器人处于奇异位姿时，因为关节空间最大速度有两种来源，则可计算出两种笛卡尔空间的最大速度，再加上用户输入的最大速度。因此，最终综合约束条件 $\dot{X}_{max}=min (\dot{X}_{max1},\dot{X}_{max2},\dot{X}_{max3})$